Hey everyone! Previously, I have covered an article on a Crash Course to Options. This resource will be an extension to that article where I will cover the basics of Greeks. Now, what are the Greeks? They are symbols assigned to various risk characteristics that an options position entails. The Greeks include Delta, Gamma, Theta, Vega and the mini Greek, Rho. Below is a summary of the 5 Greeks.
Table of Greeks

Delta
Delta is the amount an option price is expected to move based on a $1 increase in the underlying stock
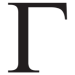
Gamma
Gamma is rate of change in an option’s delta per $1 increase in the underlying asset’s price
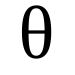
Theta
Theta is the money (value) that an option loses everyday because it gets closer to expiration

Vega
Vega is the change in the option value for every 1% increase in volatility
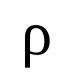
rho
Rho identifies how much an option premium may move if the risk-free interest rates increase
Delta Δ
Let’s start off with Delta. Delta is the amount an option price is expected to move based on a $1 increase in the underlying stock. Let us take a look at some characteristics of Delta
- Delta is always between -1 and 1 (between 0 to 1 for calls and -1 to 0 for puts)
- Put option’s delta is always negative (think of it as because you want the put option price to go down)
- The further out of the money (OTM) of an option, the magnitude of Delta becomes less and less. (Further away from current market, the lesser a big move has on your profit margin, less impact it has)
- Grows as option moves ITM and shrinks as option moves further OTM
- Can be interpreted as the % chance of expiring ITM (e.g. Delta of 0.4 can be thought of as 40% of the option expiring ITM). Hence -1/1 shows that the option is very much ITM.
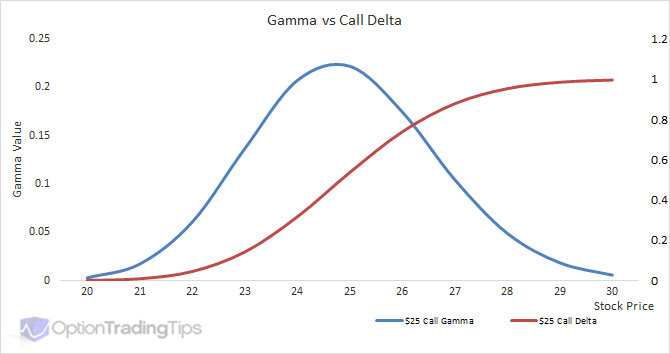
Gamma Γ
Next, Gamma is rate of change in an option’s delta per $1 increase in the underlying asset’s price. Let us take a look at some characteristics of Gamma.
- Always positive for both puts and calls
- Value of Gamma declines regardless of if you move ITM or OTM
- Highest for at-the-money (ATM) options (Small change in the underlying assets value will have a big impact on the demand for the contract)
- Gamma is what drives the increased value of your option relative to the stock price move
- Gamma is also seen as a “change in shares”
- Buying an option means you have a “long” gamma position
- Selling an option means you have a “short” gamma position
Relationship between Delta and Gamma
- For a call option, you want the underlying to increase so the option is worth more
- For a put option, you want the underlying to decrease so the option is worth more
- Analogy: Think of Delta is your speed, while Gamma is your acceleration. This means that the Gamma is the gradient of your Delta graph.
| New Delta | Underlying Increase | Underlying Decrease |
|---|---|---|
| Call and Put | Old Delta + Gamma | Old Delta – Gamma |
- Put option value and underlying price always moves in opposite direction
- Call option value and underlying price always moves in the same direction
- Put option’s Delta is negative, Call option’s Delta is positive
Theta Θ
Now moving on to Theta. Theta is the money (value) that an option loses everyday because it gets closer to expiration. Let us take a look at the characteristics of Theta
- Always negative
- Always working against you as an option buyer, but not as an option seller (i.e. Theta works in advantage of option sellers)
- Theta is bigger for those that are closer to the current strike price
- Theta (and other Greeks) are not a fixed figure, as options are priced ultimately by demand and supply
- Rate of theta decay accelerates nearing expiry
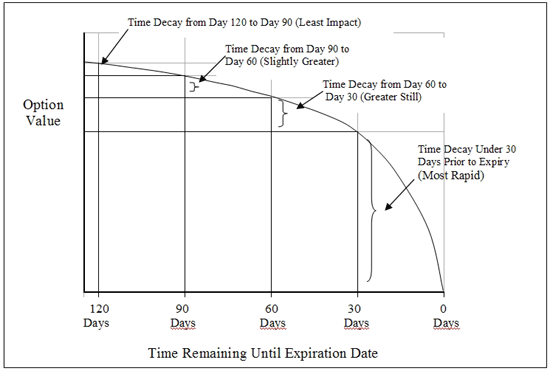
Relationship between Gamma and Theta
- A “long” gamma results in a cost of theta and vice versa (Recall that a long gamma is to buy an option)
- Characteristics
- Near term options have high Gamma and high Theta, lower cost of the option
- Longer dated options, cost less time decay (Theta) but earns less for a given move (due to lower Gamma)
Vega ν
Vega is the change in the option value for every 1% increase in volatility. Let us take a look at some characteristics of Vega:
- Always positive
- Increase in volatility can lead both ways
- Major Selloff
- Major Rally
- Closer to ATM, the larger the Vega
- options with a longer expiration may react more/more sensitive to a change in volatility (further from expiration, the higher the Vega)
- Higher Implied Volatility (IV) means higher options prices
Rho ρ : The Mini Greek
Lastly, Rho identifies how much an option premium may move if the risk-free interest rates increase. Typically, the Treasury Bills (T-Bills) are used to determine the risk-free interest rate. Take for example a put option with a price of $4 and a Rho of -0.35. If the interest rate decreases from 3% to 2%, the put option price will increase from $4 to $4.35.
Here are some characteristics of Rho:
- Call options have positive Rho, while put options have negative Rho
- This is because call options generally rise in prices as interest rates increase and vice versa.
- Most sensitive for options with long time to expiry
- Larger for options ITM and decreases as the option goes OTM
- Change in interest rates typically have a minor impact on options prices, hence Rho is not considered an important Greek
Example of how Greeks are used
In this section, I will give an example of how Greeks are used and how the value of an option changes due to various events. Hopefully, this will give you a better understanding of the Greeks.
| Call Option Price | Delta | Gamma | Theta | Vega |
|---|---|---|---|---|
| $1.30 | 0.35 | 0.06 | -0.02 | 0.07 |
Current Underlying Price: $45
Day 1: Stock moves up by $1 to $46
- Premium increases by $0.35 (due to Delta) to $1.65
- Decreases by $0.02 (due to Theta). End of day price is $1.63
Assumption on Day 1: No change in IV
| Call Option Price | Delta | Gamma | Theta | Vega |
|---|---|---|---|---|
| $1.63 | 0.35 | 0.06 | -0.02 | 0.07 |
Day 2: Stock moves up by $1 to $47, IV increases by 1%
- Premium increases by $0.35 (Delta) + $0.06 (Gamma) to $2.04
- Decreases by $0.02 to $2.02 (due to Theta)
- Increases by $0.07 due to (Vega). End of day price is $2.09
| Call Option Price | Delta | Gamma | Theta | Vega |
|---|---|---|---|---|
| $2.09 | 0.41 | 0.06 | -0.02 | 0.07 |
What if it is a Put Option?
| Call Option Price | Delta | Gamma | Theta | Vega |
|---|---|---|---|---|
| $1.30 | – 0.35 | 0.06 | -0.02 | 0.07 |
Current Underlying Price: $45
Day 1: Stock moves up by $1 to $46
- Premium decreases by $0.35 (due to Delta) to $0.95
- Decreases by $0.02 (due to theta). End of day price is $0.93
Assumption on Day 1: No change in IV
| Call Option Price | Delta | Gamma | Theta | Vega |
|---|---|---|---|---|
| $0.93 | – 0.35 | 0.06 | -0.02 | 0.07 |
Day 2: Stock moves up by another $1 to $47, IV increases by 1%
- Premium decrease by $-0.35 (Delta) + $0.06 (Gamma) to $0.64 (New Delta is $-0.35 +0.06 = $-0.29)
- Increases by $0.07 due to (Vega) to $0.71
- Decrease by 0.02 to $0.69 due to Theta. End of day price is $0.69
| Call Option Price | Delta | Gamma | Theta | Vega |
|---|---|---|---|---|
| $0.69 | – 0.29 | 0.06 | -0.02 | 0.07 |
Hope you found this short introduction to option Greeks useful! I will be updating this page whenever there is new information so do check in from time to time. In addition do check out these videos below which helped in the making of this resource. Cheers!
-Rice

